■ 「物理の壁」なんて存在しない!? ■
小竹 悟(信州大学理学部理学科物理学コース 素粒子論研究室教授)
 最近の同窓会報に「物理の壁」の話題が取り上げられており、物理数学を教えているという事から私に原稿依頼のメールが届き、余りピンと来ていない状態ながら、何かとお世話になっている同窓会に貢献できる様にと引き受けさせてもらいました。
最近の同窓会報に「物理の壁」の話題が取り上げられており、物理数学を教えているという事から私に原稿依頼のメールが届き、余りピンと来ていない状態ながら、何かとお世話になっている同窓会に貢献できる様にと引き受けさせてもらいました。
(信大物理同窓会報64号/2018年春号『シリーズ「サイエンスラウンジ」そのⅤ 誰もがぶちあたる難解な「物理の壁」について』より転載)
* * * * * * * * * * * * * *
●● 3つの仮定の下で考えてみよう ●●
ピンと来ないと書いた一つの理由は、自分の学部時代に「物理の壁」というものを感じた事がなかったからです。それは全てが分かったという事では決してなく、分からない事は沢山沢山あったのですが、それを「物理の壁」と思った事がなかったという事です。何を書こうかと運動中などにぼんやりと考えるうちに日が経ち、締切が近づいて来たので書き始めようとした時に、最近の同窓会報の「物理の壁」の記事を見ておいた方がよいと思い改めて読んで見ました。
私が書こうとしていた事がこれまでの記事の流れと多少違うなと思いましたが、色々な意見があり、それを自由に議論できる環境が大切だと思いますので、(これまでの流れを余り損なう事の無い様に多少修正しつつ)書いてみる事にします。字数は自由という提示に甘えて少しだらだらと長くなってしまった事と、(「物理の壁」の)定義や論理が必ずしも首尾一貫していない点がある事を御容赦下さい。
3つの仮定
(a) 物理を理解しようと(強く)思っている学生の話である.
(b) 大学学部教育の話である.
(c) 古き良き時代の大学ではなく、最近の大学の話である.
の下で、話を進めて行く。勿論、物理(物理(科)学科・理学科物理学コース)の話である。
●● 分かる・理解するとは? ●●
先ず、分かる・理解するとはどういう事であろうか。例えば、数学の定理を考えてみると、(意味は分からなくとも)証明を追う事ができれば定理が分かったと言うのか、(証明が追えなくても)定理が教えてくれる計算などができる様になったら分かったと言うのか、他の問題を考えている時にこの定理が適用できる事を見抜いて使う事ができる様になったら分かったと言うのか。高校で学ぶ微積分の計算(例えば三角関数の微分)は皆できるであろうが、高校生の時の理解、大学の微積分の授業を受けた後の理解、物理数学で複素関数論を学んだ後の理解、はそれぞれ異なっているであろう。
これらの例から読み取れる様に、分かる・理解するという事を話題にする際には、「どこまで」「どのレベルまで」という事を考える必要がある。「かすかにわかる」「わかったつもり」と習った微分・積分について述べてみると、微積分の定義から始まり、ドリルの様な初歩的な計算、簡単な例題、もう少し難しい問題、もっと難しい大学受験問題と進み、扱う関数も多項式から指数関数・三角関数・対数関数と増えて行き、少しずつ理解が進んでいった。定義をしっかりと覚えたとしても具体的な微積分の計算がすぐにできる様になる訳ではなく、高校での勉強(特に受験勉強)を通して少しずつ身に付いていった。
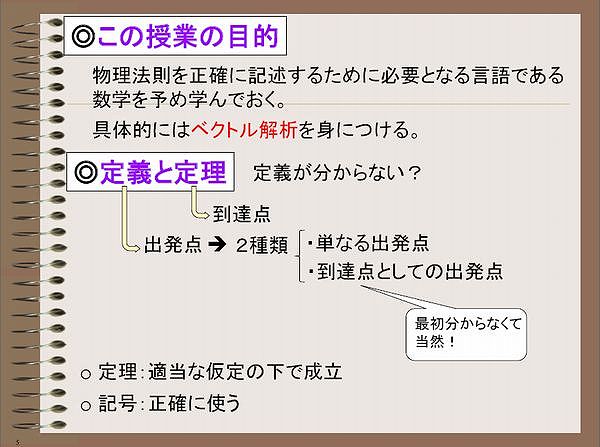
大学に入ってもそれは同じで、習った事はその後の反復練習を通して少しずつ身に付いていく。(高校と違うのは、練習にあてる時間が授業中に取られずに自分自身に任される点で、サボってしまうとどんどんと落ちこぼれて行く。) 同じ計算をやってもその理解度は高校1年、2年、3年、大学1年、2年、・・と違っている。1年後期の物理数学Ⅰではベクトル解析を扱い、勾配・発散・回転・ラプラシアンやストークスの定理・ガウスの定理などを学ぶ。これらの定義を覚え、取り敢えず計算ができる様になるというのがこの授業の目的で、それを達成すると単位がつく。
しかし、勾配・発散・回転などの計算はできる様になったものの、1年生の後期が終わった段階では、それが意味するものは何だかよく分からないという人が殆どだろう。2年生になって電磁気学を学び(3年前期まで続く)、物理現象・物理法則の中で現れる姿を見て、徐々に自分なりのイメージを持てる様になって行き、更に経験を積む事でしっくりと来る様になって行く。この段落で述べたいのは、
「新しい事を学ぶ際には慣れが必要である」
という事である。慣れと書いたが、よく理解してないのに麻痺して慣れるという意味ではなく、理解しようと努めながら経験を積んで慣れるという意味である(実際には、難しい内容に関しては麻痺して慣れるという事もありだろうが・・)。物理数学Ⅰは1年生の授業であるが、その内容の理解は1年生で終わる訳ではなく、1年生後期では単位が取れる程度、2・3年生では電磁気学に現れる式が理解できる程度、4年生では更に進んだ内容に使える程度と、「慣れ」と共に理解は進んで行く。(私の場合、ベクトル解析をよく理解できたと思えたのは、微分幾何学という数学の一分野を、数学科の授業を聞いたり、一人で又は友人と共に勉強してからであった。この場合は、より進んだ内容を勉強したので、元の話が簡単に思えたのである。)
テキストを読んですぐに理解でき色々な事ができる様な内容ならば、わざわざ大学に入って学ぶ必要はない。大学に入って4年間も学ぶのは、内容量もさることながら、身に付くまで理解するには時間が掛かるからである(4年間でも足りないであろう)。
●● 積み重ねの学問なので1年生から手頃な段差を登る練習を ●●
目の前に3mの壁があって、その上に登りたい(登らなければならない)とする。しかし、いきなりこの壁をよじ登れと言われても困ってしまうであろう。例えば、入学直後の1年生が4年生向けの問題を解いてみろと言われても、それは登れない壁にしか見えないであろう。
我々が学生に提供しているカリキュラムでは、そんな無茶をやらせる事はない。カリキュラムに沿って学んできた4年生がこの壁を見ると、その近くに必ず階段がある事に気付く筈である。階段は、段差が10cm・15cm・20cm・40cm・1m(これはもはや階段ではないが)と様々なものが見えており、段差が10~20cmといった手頃な階段を登って行けばよい。ところが在学4年目でも4年生に進級できなかった学生(4年生進級には関門がある)には、手頃な段差の階段が見えず、段差40cmの階段しか見えないため登るのに苦労する。更に4年目でも単位が殆ど取れていない学生には段差1mという階段しか見えず、登れない壁に見えてしまうであろう。
カリキュラムでは手頃な段差の階段を登るという練習を1年生から繰り返して行なっていく。そうして、1m・2m・3mといった壁(近くに階段が用意されている)を登っていく。ここでの階段を登るというのは内容を理解するという事を指しているが、上の段落で述べた様に、理解の程度には色々なレベルがあり、最初から深く理解する事は無理であり、その学年のその時点での理解ができればそれでよい。ありきたりだが、
「数学や物理学は積み重ねの学問である」
と言われており、実際その通りであろう。皆さんは入学試験に合格して一定水準の能力を持っており、カリキュラムはその人達が無理なく進める様に作られているので、カリキュラムに沿って一日一日真面目にやって行けばよい。
●● 生真面目過ぎなくて構わない ●●
その学年のその時点での理解ができればよいと書いたが、しっかりと理解しないと気が済まないと思う生真面目な人もいるだろう。そういう人は次の様に考えてもらいたい。例えば、微分の計算は当たり前の様に行なっているが、微分を定義するには極限の定義が必要で、その極限を厳密に定義するにはイプシロン・デルタ論法が必要であり、また突き詰めれば、実数の性質や集合論などの数学基礎論も必要となっていくが、おそらく普段そんな事は気にしていないであろう。数学基礎論に興味があるのならそちらに向かえばよいが、物理に興味のある皆さんに取っては、微分を用いて物理を理解する事に目を向けるべきである。新しい事を学ぶ際には分かる所と分からない所が出てくるが、分からない所に拘って止まってしまったり、時間を掛け過ぎるよりも、
「ここの所は分からないという事を記憶に留めて、先に進む」
のがよい。そして少し先に進んでから振り返ってみる。すると少し知識が付いているので分かる様になる場合がある。先に進むと更に分からない所が現れてくるだろうが、そこの所も分からないという事を記憶に留めて先に進む。そして振り返る。この繰り返しである。数学の定理においても、証明までしっかりと理解して使うのが最善だが、証明が分からなくても、難しい証明は数学者に任せて、定理の内容を正しく理解して使えればそれでよいのである。(定理の内容をいい加減に覚えて使うのはダメ。)
●● 分からない原因は ●●
分からない所がある時に、嫌になって授業をサボったりするとますます分からなくなり、単位を落とす事につながっていく。(1、2年生の授業で)分からなくなる原因は何であろうか。上の段落に出てきた、高校生の時に微積分が分かる様になるまでにどの位勉強したかを思い出そう。高校で1年以上掛けて教えられた内容量と同程度の量の内容が、大学の授業では半期(実際には4ヶ月)に押し込まれているにも拘わらず、練習時間は授業時間中には殆ど取られない。練習は一人一人に任されているが、高校で微積分につぎ込んだ時間と比べると明らかに短いであろう。分からなくなる原因は、単純に、
「勉強不足である」
と言えよう。高学年の授業での分からないの原因は、単純に勉強時間の不足というだけではなく勉強の質の問題も入ってくるだろうが、低学年では勉強時間が最大の要因であろう。
●● 単位を再び落としてしまう人には2種類のタイプがいる ●●
数学や物理学は積み重ねの学問であると上に述べたが、それは、積み重ね損なうとその後に影響が及ぶ事を意味する。先ず何より、その授業の単位を落としてしまう。1年生で単位を落としてしまう原因は、多くはサボってしまった事による。落とした単位は翌年再履修し、それで単位を取れればよいが、また落としてしまう人がいる。(本当は単位が取れるか取れないかよりも、内容をちゃんと理解したかどうかの方が大切であるが、卒業のためには単位取得は大切である。)単位を再び落としてしまう人には2種類のタイプがいる様である(本当にそうなのかは分からないが、私にはそう感じられる)。一つは前回の反省を全くしていない人で、また同じ様にサボって落としてしまう。こんな事をしていてはどうしようもない。
もう一つは前回の反省をするのだが、同級生よりも遅れを取ってしまったとの焦りの気持ちから、無理な計画を立てて自滅してしまう人である。先程は壁を登る事に譬えたが、今度は長い距離を歩く(走る)事に譬えてみよう。我々のカリキュラムでは学生に無茶をさせる事はなく、例えば、10kmを2時間で走破するという課題を与えたとする。この課題を素直にやればよいのに、同級生に遅れを取ったと焦っている人はその遅れを取り戻そうと、10kmを1時間で走破しようとする。しかし2時間でダメだった人が1時間でやり遂げるのは望み薄である。中には、10kmを10分間で走破する計画を立ててしまう人もいるが、これは人類には不可能である。そして計画が失敗すると自信を失って、授業から足が遠のいてしまう。また、授業に出たとしても、去年聞いた話だと高をくくって真面目に取り組まず、結局は分からないままになってしまう人が多い。再履修をする事になった場合は、
「初めて聞く授業だと思って、真剣に取り組む」
事が必要である。遅れを取り戻そうという気持ちは分かるが、理解するのにはどうしても時間が掛かるのであるから、焦らずにやっていくしかない。その際に一人ぼ
っちでやる必要はなく、次の段落で見るように回りの人に助けてもらえばよい。
●● 質問をしよう ●●
理解するのは最終的には自分自身であるが、そこに到る過程においては一人である必要はない。先ずは自分で考えてみる必要があるが、分からない場合にはすぐに友人・先輩・先生に聞いてみるのがよい。教えてもらって理解できればそれでよいのである。大人になると、こんな事を質問をすると恥ずかしいなどと思う様になってしまうが、学生の皆さんは、分からないのが当たり前で質問するのが仕事だ、くらいに思ってもらいたい。恥ずかしいのは分からないのにそのまま放っておく事の方である。本原稿はシリーズ「サイエンスラウンジ」の一環であるが、
「サイエンスラウンジを利用する」
のもお勧めである。チューターとなった4年生が、質問に来て欲しいと皆さんを待っているのだから、気軽に質問できるであろう。一人で勉強するだけでなく、友人と共に勉強する、更には自主ゼミに参加・企画へと進み、積極的に学んでもらいたい。
●● ここまでのまとめ ●●
ここまでの話をまとめてみよう。カリキュラムは学生に無茶をさせる事なく、無理なく進める様に用意されているので、カリキュラムに沿って一日一日真面目に取り組んでもらい、理解度についてはその学年のその時点で求められる程度で構わないという認識の下では、何が何だか分からないという
「「物理の壁」は存在しない!」
とまとめられよう。但し、仮定(a)(b)(c)の下の話である。「物理の壁」という壁を自分で作って、それに縛られる必要はないのである。
●● 結局、物理学を究める階段は自らが作って登って行くもの ●●
それでは仮定(a)(b)(c)が無くなった場合にはどうなるであろうか。順に見てみよう。
※ 仮定(a)が外れた場合:
物理に興味があるので入学したという人が大部分だが、中には模試の成績で判断して合格できるからという理由で入ってくる人もいよう。その様な人でも入学後に興味を持つ場合もあれば、逆に入学前に持っていた興味を失ってしまう人もいる。長続きする行動の原動力としては、(1)本能(食事、睡眠など)(2)興味(物理が好き、運動が好きなど)(3)必要(お金を稼ぐために働くなど)があり、少なくとも一つは必要である。私などは、好きな物理が仕事になっているので(但し、好きな事ばかりをやってはいられない)、恵まれていると言えよう。
教える立場ならば、興味を失ったとしてもお金を稼ぐための仕事として教える事はできるが(その様な先生には教えてもらいたくないが)、学生の場合には、興味を失った時に授業料を払ってまでやり続ける事は困難であろう。興味を失ってしまった学生に取って物理を学ぶ事は苦行でしかなく、物理を理解しようという気力が無くなっているので、そこら中に「物理の壁」が立ちはだかるだろう。
※ 仮定(b)が外れた場合:
学部教育では既に分かった事柄を教えている。それに対して研究はと言うと、未だ誰も知らない、分かっていない事柄を明らかにしようとするものであり、「壁」だらけである。3mの壁、5mの壁、10mの壁、100mの壁、上が見えない壁と様々である。また、壁の近くを見ても階段は用意されていない。階段は自らが作って登って行くのである。階段を作り易い壁もあれば、硬くて歯が立たない壁もある。階段を作る技術は様々で、綺麗な階段を作る人、素早く階段を作る人、新しい機械を持ち込む人、斬新なアイデアを思いついて一足飛びに登る人、がいる。一人で頑張って階段を作る人もいれば、友人達と協力して作る人達、更には何千人ものグループを組織して大きな壁に挑む人達もいる。一つの壁に複数の人・グループがそれぞれ階段を作って一番乗りを目指している。途中までは階段が作れたものの、それ以上は作れずにそこで立ち止まってしまった人達もいる。階段を作って壁を登って行くのは大変な作業だが、上手くいった時の達成感は格別である。
さて、大学院教育はと言うと、学部教育と研究の中間にある。既に分かった事柄を教わり知識を増やしつつ、研究に乗り出していく。既に分かった事柄を教わる部分はカリキュラムに沿っていけば何とかなるが、研究に入る部分はカリキュラムでは何ともならず、そこには「物理の壁」が存在する。
※ 仮定(c)が外れた場合:
古き良き時代の大学の授業は、担当する先生によって大きな違いがあるだろうが、大学生として理解してもらいたいと先生が思う内容を、学生の理解度を無視して、一方的に話していた様に思う。学生の自主独立性を養うという点で効果があったかもしれないが、落ちこぼれてしまう学生が大量に現れたであろうし、今の大学でその様な授業をやれば批判にさらされてしまう。
クラスの半数が不合格となってもそれは学生の理解不足だ、多くの学生が勉強しなくてもそれは学生がサボっているからだ、という言い訳は今の大学では通用しない。クラスの半数が不合格となればそれは先生の教え方が悪いからだ、多くの学生が勉強しなければそれは先生の指導が悪いからだ、となる。各先生は各授業で工夫を凝らしているし、物理全体としてもカリキュラムに改善を加えてきた。
カリキュラムは、学生に無茶をさせる事なく、真面目にやれば無理なく進める様なものを用意している。学生に迎合する訳ではないが、最初は手取り足取りから始めて、徐々に手放して自主独立性を養う様にしている。現在のカリキュラムが最善という訳ではなく、常に改善を加えようと心掛けている。古き良き時代の大学の授業は、そのカリキュラムというよりも個々の授業での教え方に些か問題があり、いくら意欲のある学生でも、無茶を強いられたために「物理の壁」が存在していたのだろう。
●● そうは言っても「物理の壁」は存在する? ●●
私の主張は「物理の壁」は存在しない(仮定(a)(b)(c)の下で)という事だった。しかし、優秀な学生ならばそうかもしれないが、そうでない学生に取ってはやはり「物理の壁」は存在するのではないかと反論する方もおられるであろう。そう強く言われればその通りかもしれないし、単に程度の問題かもしれない。私が伝えたいのは、
「「物理の壁」という壁を自分で作ってしまって、諦めてしまうな」
という事である。
●● おわりに ●●
原稿依頼のメールを今一度見てみますと、
「さて、当同窓会報において、いわゆる「物理の壁」についてさまざまな方に書いていただいております。大学1、2年次に数学的要素が必要となり急に難しくなる大学の「物理の壁」をどう克服すればいいか。多くの物理専攻生が悩み苦しむところです。小生の世代の卒業生も、ほとんどの者が未消化のまま卒業したといってもいい状態です。そこで、物理数学を教えておられる小竹先生に、この問題についてどうお考えなのか、克服するための方法(近道)はあるのか、アドバイスなどをいただけないかと考えた次第です。」
とあり、どう考えているかについてはある程度書いたと思いますが、克服するための方法については余り答えられていないかもしれません。一年後期の物理数学Ⅰでは、一回目の授業の初めに、授業時間を削ってでも伝えるべきだと考えて、心構えの話をしています。その話のスライド(の一部分)を付けて、回答の代わりにしたいと思います。
スライドにはキーワードしか書かれていませんが、最近の学生は皆一度は聞いている筈なので、話を思い出せるのではないかと思います。(私の話を聞いた事がない方は、済みませんが、適当に説明文章を補って御覧下さい。)上の文章やこのスライドを参考にして、皆さんが勉強に励んでくれる事を願っています。
▼小竹先生が1年後期の「物理数学Ⅰ」の講義の最初に紹介しているスライド「心構え」(の一部分)





 まで。
まで。